Фрактальность природных и архитектурных форм

Исаева В.В., Касьянов Н.В.

Аннотация

С целью выявления общности и специфических отличий морфогенеза в природе и архитектуре рассмотрены некоторые здания и сооружения в сопоставлении с природными формами и фрактальными моделями. Архитектурные формы более регулярны, чем природные, и вовлекают малое число повторов с их вариациями.

Some buildings and constructions are considered in comparison with natural forms and fractal models in order to reveal common and specific features in architectural and natural morphogenesis. Architectural forms are more regular than forms of nature, and involve few iterations with variations.

В течение последних десятилетий стремительно развивается новая обширная область междисциплинарных исследований, включающая нелинейную динамику, фрактальную геометрию, теорию самоорганизации. Междисциплинарный подход существенно раздвигает рамки научных исследований, помогая выявить общие черты морфогенеза в живой и неживой природе. Фрактальные алгоритмы (правила построения) в природе и творчестве человека открыл Бенуа Мандельброт (B. Mandelbrot). Одна из важнейших характеристик фрактала – масштабная инвариантность (самоподобие в широком диапазоне масштабов). Дробное значение фрактальной размерности характеризует степень заполнения пространства фрактальной структурой, тогда как значение лакунарности представляет собой меру неоднородности структуры фрактала [10].

Множество процессов, происходящих в природе и обществе – от космических до социальных и физиологических, – характеризуется хаотической фрактальной динамикой [2, 9, 10, 12]. Фрактальность природных объектов подтверждается возможностью построения весьма правдоподобных компьютерных ландшафтов виртуального мира на основе простых фрактальных программ, в которых приближение к реальности достигается некоторой степенью нерегулярности путем введения случайных чисел. Морфогенез растений также успешно имитируется подобными программами. Моделирование морфогенеза животных на всех уровнях их организации – динамично развивающаяся область биологии. Биологические структуры сложной пространственной организации могут быть количественно охарактеризованы путем определения фрактальной размерности, служащей показателем морфологической сложности этих структур [8]. Вовлечением фрактальных алгоритмов в биологический морфогенез обеспечивается сжатое генетическое кодирование. Фракталоподобные структуры живой природы характеризуются ограниченной шкалой повторов и менее хаотизированы по сравнению с фракталами неживой природы; как правило, это мультифракталы, т.е. неоднородные фракталы.

Использование подходов фрактальной геометрии позволяет выявить сходство ряда живых и неживых объектов – как природных, так и созданных человеком. Один из примеров такого параллелизма формообразования дает сопоставление конструкций геодезических куполов с организацией молекул фуллеренов, макромолекулярных комплексов клеток многоклеточных животных и скелетных структур радиолярий (рис. 1). Строительные конструкции геодезических куполов были запатентованы в 1954 г. Р.Б.Фуллером (1895–1983), американским изобретателем, архитектором и философом [17]; в нашей стране такими разработками занимался М.С.Туполев. Геодезические купола могут быть образованы сложной сетью треугольников, которые формируют поверхность, близкую к сферической (рис. 1а). Повторные подразделения на треугольники, характерные для геодезических куполов, образуют фрактальный алгоритм. Конструкции с таким триангуляционным разбиением оказались не только перспективными в архитектуре, но и очень сходными с природными формами. В 90-е годы прошлого века было получено новое вещество – фуллерит, состоящее из молекул углерода, фуллеренов (этимология названий фуллеренов и фуллерита весьма прозрачно связана с именем Фуллера). Фуллерит – аллотропная модификация углерода [7], третья кристаллическая форма углерода (две ранее известные формы – графит и алмаз). Молекулы фуллеренов представляют собой замкнутую поверхность в форме сферы или сфероида, на которой располагаются атомы углерода (рис. 1б). Конструкции геодезических куполов подобны и некоторым биологическим структурам, например макромолекулярным комплексам клатрина (рис. 1в), сети пучков актиновых филаментов клеток многоклеточных животных (рис. 1г) и скелетам некоторых радиолярий, одноклеточных организмов (рис. 1д).

Изобразительному искусству и музыке также свойственны фракталоподобные характеристики [1, 10, 16]. Некоторые примеры использования художниками повторяющихся в разном масштабе элементов, т.е. фрактальных множеств, приведены Б.Мандельбротом [10]. Исследования традиционной музыки Японии, Индии, народных песен России, американских блюзов, музыки Баха, Бетховена, Дебюсси, Штрауса привели к выводу о том, что музыка имеет общие черты с динамикой природных процессов, имитируя природные изменения нашего мира во времени [1, 16, 19]. Произведение искусства приятно и интересно при условии, что оно не слишком однообразно и в то же время не таит в себе слишком много сюрпризов; музыка приятна, если в ней присутствуют изменения тональности во многих масштабах частот и изменения ритма хотя бы в нескольких масштабах времени [16]. Компьютерное изображение множества Мандельброта можно перевести в звуки и получить музыку с повторяющимися и сменяющимися «темами». Переложение электрокардиограммы человека в звуки дает «песни сердца», музыку, синтезированную по алгоритму хаотических фракталов кардиограммы (см. [8]).

Применение повторяющихся в разном масштабе самоподобных форм, т.е., в сущности, фрактальных правил построения, широко распространено и в архитектуре. Известное уподобление архитектуры застывшей музыке (И.В.Гете) глубоко обоснованно: и музыка, и архитектура фрактальны. Произведения архитектуры включают в себя многие масштабы длины и элементы самоподобия: подобие частей и целого, подчиненность отдельных элементов целому (рис. 2). Архитектурные фрактальные структуры более упорядочены, чем природные. Фрактальность многих архитектурных форм весьма очевидна и лежит буквально на поверхности (как правило, на фасаде). Мандельброт первым написал о фрактальности архитектуры и привел архитектуру здания Парижской оперы, произведения «изящного» искусства (архитектор Ш.Гарнье), как пример фрактального творения [10]. М.Шредер в качестве примера самоподобия в архитектуре называет замок Кастель дель Монте, построенный по собственному проекту императором Священной Римской империи Фридрихом II. Этот замок представляет в плане правильный восьмиугольник, к вершинам которого пристроены восемь мощных башен, каждая из которых также имеет в плане форму правильного восьмиугольника [16].

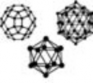
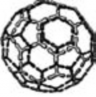
Рис. 1. Фрактальное разбиение: а – макет геодезического купола; б – строение молекул фуллеренов; в – клатриновая сфера [13]; г – система пучков актиновых филаментов цитоскелета; д – скелет одной из радиолярий [14]

Рис. 2. Самоподобие форм в архитектуре: а – здание Исторического музея в Москве; б – здание почтамта во Владивостоке; в – индийская храмовая архитектура, комплекс в Кхаджурахо [15]

Рис. 3. Фрактальные прообразы и архитектура пирамидальных фасадов, колоколен: а – «салфетка» Серпинского, построенная из квадратов [9]; б – фрагменты фасадов готических зданий Германии [3]; в – колокольня (г. Кашира)

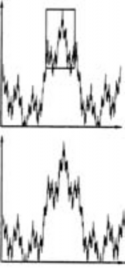
Рис. 4. Сходство очертаний графика функции Вейерштрасса (а) и силуэта а Миланского собора (б)

Принципы фракталоподобного формообразования в архитектуре применяются с давних времен, но лишь к концу XX в., после появления книг Мандельброта, использование фрактальных алгоритмов в архитектурном морфогенезе становится осознанным. Ч.Дженкс [4, 20] описал переход к новой парадигме в архитектуре под влиянием наук о сложных системах, включающих фрактальную геометрию и нелинейную динамику. Несколько ключевых зданий, построенных Ф.Гери (Frank Gehry), П.Эйзенманом (Peter Eisenman) и Д.Либескиндом (Daniel Libeskind), выглядят как первые проявления этой новой архитектурной парадигмы. Современные архитектурные течения, оперирующие образами сложных поверхностей, математически описываемых нелинейными уравнениями, можно условно называть нелинейной архитектурой. Ч.Дженкс [4, 20] и И.А.Добрицина [5] писали о нелинейности и фрактальности архитектуры в общей декларативной форме. Фрактальная геометрия Б.Мандельброта в определенной мере использована для анализа архитектурных форм в книге К.Бовилла [19], единственной к настоящему времени монографии о фракталах в архитектуре, в которой собственно архитектуре посвящена меньшая часть книги. В ряде статей и сайтов Интернета отмечены повторяющиеся в разных масштабах элементы архитектуры готических соборов, стиля барокко, индийских храмов, проведен анализ повторов в классических ордерных формах.

Фрактальная формализация применена Бовиллом [19] к рядам строений вдоль улиц и для определения фрактальной размерности некоторых архитектурных сооружений (в том числе Ф.Л.Райта и Ле Корбюзье) методом подсчета квадратов; такой анализ устанавливает эстетическое обоснование оценки архитектурного дизайна, позволяющее дать рекомендации для ухода от мертвящей монотонности стандартной архитектуры. Однако попытки количественным образом связать высокое значение фрактальной размерности (отражающее дробность деталировки) с архитектурной выразительностью не слишком много дают для понимания фрактальных правил построения архитектурных форм. Значение фрактальной размерности может служить лишь формальной характеристикой пространственной сложности объекта, не учитывающей более важные качественные характеристики. Хотя обычно с фракталами ассоциируется богатство форм, фракталы могут быть и эстетически неинтересны, даже скучны. Напротив, в архитектуре есть сооружения, практически лишенные фрактальных характеристик и при этом весьма выразительные – например, массивные нелинейные формы. Фрактальные прообразы архитектурных форм фактически еще не были показаны.

Целью нашей работы был поиск простейших графических фрактальных образов, визуализирующих некоторые архетипы фасадов, планов и трехмерных архитектурных форм, и привлечение имитационного компьютерного моделирования для качественного, а не количественного анализа фрактальных по существу алгоритмов архитектурных сооружений – как правило, не осознававшихся их архитекторами и строителями в терминах фрактальной геометрии. В более широком аспекте эта задача составляет часть проблемы выявления параллелизма формообразования в столь различных мирах, как неживая и живая природа, с одной стороны, и созданные человеком формы – и реальные архитектурные, и виртуальные (компьютерные) – с другой. Современный научный подход с применением фрактальной геометрии, а также топологии и нелинейной динамики способен выявить здесь множество сходных направлений и решений морфогенеза, включая не раскрытые ранее аспекты формообразования и создание потенциально новых архитектурных форм. Ссылаясь на Мандельброта: «графическое представление – чудесное средство для сопоставления моделей с реальностью» [10, с. 41], рассмотрим некоторые графические фракталы в качестве прототипов архитектурных фасадов и планов.

Алгоритм Серпинского (так называемая салфетка Серпинского, построенная в данном случае из квадратов) на первых этапах построения дает прообраз таких культовых сооружений, как ступенчатые пирамиды; вытянутые по вертикали здания подобного архетипа – храмовые и крепостные башни, колокольни (рис. 3 а–в). Разумеется, бесконечные повторы какой-либо структуры в архитектуре невозможны, реальная архитектура обычно содержит немногие повторы, поэтому фрактальные модели, имитирующие архитектурные сооружения (или раскрывающие «генетический код» архитектурных объектов), – это протофракталы (термин Мандельброта для фрактальных структур с немногими повторами). Кроме того, в архитектуре, как и в музыке, редко встречаются точные повторы, обычны же вариации темы, образа.

Для силуэта храмов с множеством вертикальных повторяющихся элементов неким метафорическим прообразом может послужить график функции Вейерштрасса (рис. 4 а, б) – классической фрактальной функции, не имеющей производных ни в одной точке (соответственно на графике нельзя провести касательную ни к одной точке), открытой в конце XIX в. Несомненно, архитекторы и строители Миланского и подобных соборов не ведали о функции Вейерштрасса, и мы не утверждаем, что силуэтные линии собора точно следуют графику функции – этот график дает лишь визуальную метафору подобных архитектурных форм.

Множество Кантора – еще один фрактальный алгоритм, пригодный для описания архитектурных форм с симметрично расположенными частями разной высоты, что весьма обычно в архитектуре (простейший архитектурный прием – в средней части здания возвышается уменьшенное подобие всего здания). Фрактальная структура классического множества Кантора дискретна, тогда как в качестве архитектурных прообразов более пригодны связные фракталы, например «салфетка» Серпинского. Соединение дискретных участков множества Кантора дает связный фрактал (гребень Кантора, рис. 5б) – прообраз «сталинской высотки» и подобных зданий. Множество Кантора с вариациями лакунарности (рис. 5в [18]) можно модифицировать простейшим образом, получив, например, графический морфотип (рис. 5 в, г), сходный с архитектурными формами индийских храмов. Фрактальный алгоритм построения дискретного множества Кантора сходен с алгоритмом формообразования дихотомически ветвящегося дерева – связного фрактала. Перевернутое дихотомическое дерево – обобщенный «архитектурный код» морфогенеза устремленных ввысь культовых сооружений, иерархичность построения которых выражает идею присутствия высших сил.

Морфогенез нелинейных фракталов порождает динамику образов, претерпевающих бесконечные метаморфозы в виртуальном пространстве, с возникновением сложных форм, сходных с биологическими и архитектурными. Архитектурный декор, узоры орнаментов решеток и оград нередко напоминают нелинейные фракталы (рис. 6).

Фрактальные черты церковного многоглавия могут быть рассмотрены на примере шедевра русского деревянного храмового зодчества – знаменитой Преображенской церкви Кижского погоста в Карелии (рис. 7а). Построенная одним из авторов компьютерная модель визуализирует расположение глав Преображенской церкви (рис. 7 б, в). Многоглавые деревянные церкви русского севера составляют морфологически родственный ряд: прототипом Преображенской церкви Кижского погоста (1714 г.) послужила Покровская церковь Вытегорского погоста в селе Анхимово Вологодской области, построенная в 1708 г. [11] и погибшая от пожара в 1963 г. Расположение и размеры куполов многоглавых церквей, условно показанные в одной плоскости плана с осевой симметрией, в самом общем виде сводятся к простому фрактальному алгоритму варианта «салфетки» Серпинского (рис. 7г).

Один из универсальных фрактальных алгоритмов, спиральный, широко распространенный в неживой (от траекторий элементарных частиц до циклонов и галактик) и живой природе (раковины моллюсков, рога копытных, завитки побегов растений), а также в архитектуре и дизайне (рис. 8), дает множество сходных решений морфогенеза. Трехмерная реализация спирального декора в виде параллельных либо раскручивающихся во встречных направлениях и пересекающихся спиралей воплощена главами храма Василия Блаженного (рис. 8а). «Храм Василия Блаженного являет собой причудливый фрактал золотого сечения, определяемый по меньшей мере восемью членами ряда золотого сечения» [1, с. 243]. Аккорды золотых пропорций и других фрактальных соотношений создают архитектурную симфонию этого храма.

Архитекторам известны такие реализации трехмерного спирального алгоритма, как башня Татлина (модель памятника III Интернационалу) и подобная конструкция спирального завершения здания на Патриарших прудах (рис. 8е).

Визуальная интерпретация «угла золотого сечения» дает фрактальный алгоритм, проявляющийся в живой природе, орнаментах и архитектуре. Построенное с помощью компьютера изображение «подсолнечника» (рис. 8б), где в качестве углового приращения используется шаг, равный «золотому углу», весьма близко к реальной картине расположения семян подсолнечника (рис. 8г), менее упорядоченной по сравнению с идеальной компьютерной моделью. Подобное расположение, называемое филлотаксисом (филло – лист, таксис – движение), характерно для листьев на стебле (или их производных), для чешуек шишек хвойных растений; при этом число рядов, закрученных в одном направлении, и число рядов, закрученных в другом направлении, составляют два соседних числа Фибоначчи [13]. На субклеточном уровне подобная особенность проявляется в расположении димеров тубулина в микротрубочках – структурах цитоскелета [13].

Простейшей и наиболее общей трехмерной фрактальной моделью далеко не красивых типовых зданий-коробок может служить «губка» Менгера (рис. 9а), структура внутреннего пространства которой показана на рис. 9б. В самой общей форме можно сказать, что прямоугольники окон подобны целому прямоугольному зданию, а параллелепипеды внутренних помещений – всей «коробке» здания. Несомненно, даже самый примитивный панельный дом построен не в точности по алгоритму «губки» Менгера, однако фрактальная геометрия включает объекты, повторяемый в разном масштабе элемент которых может быть дополнительно деформирован, изменен в соответствии с мультифрактальной программой построения. Фрактальное здание может быть построено из брусков-параллелепипедов (и включать пустоты-параллелепипеды), которые можно сдвигать, поворачивать, сжимать: фрактальные алгоритмы допускают сжатие, поворот, нелинейные преобразования исходной формы. При хаотизации таких алгоритмов, некотором нагромождении преобразований возникают формы, сходные с архитектурой постмодернизма и деконструктивизма.

Итак, для разных типов архитектурных сооружений можно найти фрактальный аналог, двумерный или трехмерный, и тем самым выявить их фрактальный алгоритм. Такие модельные фракталы, как множество Кантора, губка Менгера, могут послужить вполне адекватными моделями архитектурного морфогенеза. Разумеется, в отличие от относительно простых и регулярных геометрических и компьютерных фракталов с бесконечным повторением одной и той же формы, в архитектуре применяются правила построения с использованием ограниченного числа повторов, сменой правил их построения, нарушением строгого подобия введением множества вариаций, т.е. используются протофракталы, мультифрактальные и нерегулярные алгоритмы.

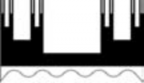
Рис. 5. Множество Кантора как прообраз архитектурных форм: а – множество Кантора; б – гребень Кантора [16]; в – множество Кантора с различной лакунарностью [18]; г – его простейшее преобразование

Рис. 6. Нелинейные фракталы и сходные с ними формы декора металлических оград: а, б – множества Жюлиа [12]; в – фрагмент множества Мандельброта [12]; г – узор решетки балкона Владивостокского ГУМа; д – решетчатая створка ворот в стиле рококо в Вюрцбурге, Германия [3]

Рис. 7. Церковное многоглавие и фрактальная модель: а – Преображенская церковь Кижского погоста; б, в – компьютерная модель этой церкви: фрагмент фасада (б), фрагмент плана кровли (в); г – вариант «салфетки» Серпинского [6]

Рис. 8. Спиральный алгоритм и формы природы, архитектуры и дизайна: а – собор Василия Блаженного; б – компьютерная модель филлотаксиса [2]; в – логарифмическая спираль; г – филлотаксис подсолнечника (для наглядности часть семян удалена); д – спиральный узор ограды (особняк Рябушинского в Москве); е – спиральное завершение здания на Патриарших прудах

Рис. 9. Трехмерная модель «губки» Менгера: а – внешний вид; б – структура внутреннего пространства

Как правило, поиск формул гармонии и красоты архитектурных форм проводится в ходе анализа уже созданных выдающимися мастерами творений. Известно, что представление о знаменитом золотом сечении, примененном Фидием при возведении Парфенона, появилось два века спустя в «Началах» Евклида, а сам термин «золотое сечение» был введен Леонардо да Винчи более чем через тысячу лет. Как использование фрактальных правил построения в архитектуре с древнейших времен, так и применение золотого сечения, разумеется, не было осознанным в терминах более поздних концепций и далеко не всегда оказывалось математически выверенным; в поиске и создании художественно выразительных пропорций архитекторов вели их интуиция и чувство гармонии. И в наше время архитекторы далеко не всегда осознают повсеместность фрактального построения архитектурных форм подобно тому, как персонаж Мольера не знал, что говорит прозой.

Фрактальный подход – не панацея, как писал сам Мандельброт, и вовсе не новая эра в истории человечества, а лишь новый, но достаточно эффективный способ анализа, а потенциально – и проектирования архитектурных форм, который может существенно обогатить язык архитектурной теории и практики.

Знаменитый испанский архитектор А.Гауди дал новую интерпретацию готических форм в своем соборе Святого Семейства (Sagrada Familia) – форм, подобных природным; Гауди ушел от евклидовой геометрии, от симметрии и регулярности. Фракталоподобные формы собора, подобного песчаному замку, представлены хаотическими, нерегулярными фракталами, свойственными природе. Современные представления нелинейной науки порождают новую концепцию соотношения упорядоченности и хаоса как состояния, включающего элементы непредсказуемости, нерегулярности, таинственности, подобные богатству и неповторимости природных форм. Использование концепций нелинейной динамики открывает перспективу корректного анализа соотношения регулярности и нерегулярности, случайности, асимметрии. Эстетика нелинейных форм с элементами случайности формулируется Г.Айленбергом: «Почему все же силуэт изогнутого бурями дерева без листьев на фоне вечернего неба воспринимается как нечто прекрасное, а любой силуэт высокофункционального университетского здания таким не кажется, несмотря на усилия архитектора? ...Наше ощущение прекрасного возникает под влиянием гармонии порядка и беспорядка в объектах природы – тучах, деревьях, горных грядах или кристалликах снега. Их очертания – это динамические процессы, застывшие в физических формах, и определенное чередование порядка и беспорядка характерно для них. В то же время наши промышленные изделия выглядят какими-то окостеневшими из-за полного упорядочения их форм и функций, причем сами изделия тем совершеннее, чем сильнее это упорядочение. Такая полная регулярность не противоречит законам природы, но сейчас мы знаем, что она нетипична даже для весьма «простых» естественных процессов. Наука и эстетика согласны в том, что именно теряется в технических объектах по сравнению с природными: роскошь некоторой нерегулярности, беспорядка и непредсказуемости» [12, с. 159–160].

Тенденция органического встраивания сооружений в природное окружение, интеграция природного и антропогенного ландшафта проявляются в подобии линий, поверхностей и форм в архитектуре и дизайне природным формам. Эта тенденция ярко выражена в стиле модерн и «органической» архитектуре. Широко применявшиеся в начале XX в. в архитектуре модерна пластичные, «текучие», асимметричные, биоморфные линии, поверхности, «струящийся» растительный декор, рельефные изображения голов придают зданиям сходство с живым развивающимся организмом, имитируют нерегулярность природных форм.

Архитектуре конца XX в. также свойственно использование биоморфных метафор – антропоморфных, зооморфных, фитоморфных, а также пластичных геоморфных форм, как бы вырастающих естественным образом из земли, с органичной интеграцией архитектуры и природного ландшафта. В наше время приходит более глубокое осознание единства природной и антропогенной среды и единства принципов формообразования в «живой» и «неживой» природе, подкрепляемое концепциями нелинейной науки. Современный научный подход может быть успешно применен для поиска архитектуры, адекватной гармонии порядка и хаоса природной среды, архитектуры, которая может стать смысловой доминантой в природном и историческом контексте, духом места (genius loci).

Литература

1. Волошинов А.В. Об эстетике фракталов и фрактальности искусства // Синергетическая парадигма. Нелинейное мышление в науке и искусстве. М.: Прогресс-Традиция, 2002. С. 213–246.

2. Газале М. Гномон: от фараонов до фракталов. М.; Ижевск: Регулярная и хаотическая динамика, 2002. 271 с.

3. Грубе Г.-Ф., Кучмар А. Путеводитель по архитектурным формам. М.: Стройиздат, 1995. 216 с.

4. Дженкс Ч. Новая парадигма в архитектуре // Проект International. 2003. № 5. C. 98–112.

5. Добрицина И.А. От постмодернизма к нелинейной архитектуре. М.: Прогресс-традиция. 2004. 416 с.

6. Заславский Г.М. Физика хаоса в гамильтоновых системах. М.; Ижевск: Ин-т компьютерных исслед., 2004. 286 с.

7. Золотухин И.В. Фуллерит – новая форма углерода // Соросов. образоват. журн. 1996. № 2. С. 51–55.

8. Исаева В.В. Синергетика для биологов: вводный курс. М.: Наука, 2005. 158 с.

9. Кроновер Р.М. Фракталы и хаос в динамических системах. М.: Постмаркет, 2000. 350 с.

10. Мандельброт Б. Фрактальная геометрия природы. М.: Ин-т компьютерных исслед., 2002. 856 с.

11. Орфинский В.П. К вопросу о национальном своеобразии культового зодчества России // Христианское зодчество. Новые материалы и исследования / ред. И.А.Бондаренко. М.: Едиториал УРРС, 2004. С. 125–180.

12. Пайтген Х.-О., Рихтер П.Х. Красота фракталов. Образы комплексных динамических систем. М.: Мир, 1993. 176 с.

13. Пенроуз Р. Тени разума. М.; Ижевск: Ин-т компьютерных исслед., 2005. 688 с.

14. Петрушевская М.Г. Радиолярии мирового океана. Л.: Наука, 1981. 405 с.

15. Смолина Н.И. Традиции симметрии в архитектуре. М.: Стройиздат, 1990. 344 с.

16. Шредер М. Фракталы, хаос, степенные законы. М.; Ижевск: Регулярная и хаотическая динамика, 2001. 527 с.

17. Baldwin J. Bucky works. N. Y.: Wiley, 1996. 243 p.

18. Blumenfeld R., Mandelbrot B.B. Lévy dusts, Mittag-Leffler statistics, mass fractal lacunarity, and perceived dimension // Phys. Rev. 1997. Vol. 56, N 1. P. 112–118.

19. Bovill C. Fractal geometry in architecture and design. Boston; Basel; Berlin: Birkhäuser, 1996. 195 p.

20. Jencks Ch. New science = new architecture // Architect. Design. 1997. Vol. 67, N 9/10. P. 7–11.