Формирование градостроительной концепции «исчисляемый город»
А. А. Ленц
Московский архитектурный институт (государственная академия), Москва, Россия
Аннотация
В статье рассмотрены «большие» и «малые» модели исчисления города: гравитационная модель Рейли, энтропийная модель, транспортная модель, Парадокс Доунса-Томсона, Постулат Льюиса-Могриджа, Парадокс Браеса, демографический потенциал, стоимостной подход. Рассмотрены достоинства и недостатки этих концепций, дана оценка научно– прикладной значимости этих моделей на основе анализа модели Форрестера и структурно-функционального подхода к анализу территорий Москвы и Ленинграда 1980-х годов. Предложена новая классификация концепций «исчисляемого города» по типу конечного получаемого продукта: оценочные, прогностические и оценочно– прогностические.
Проблема формирования модели города всегда стояла перед архитекторами и никогда не вызывала сомнений в своей актуальности и злободневности в архитектурно– градостроительной практике. Философия городского пространства формировалась на мировоззренческой основе представлений зодчих о соотношении части и целого как необходимом условии формирования верных решений в любом масштабе, будь то градостроительный план или малая архитектурная форма.
Однако до внедрения ЭВМ архитектор-градостроитель формировал социально– экономическую модель города, опираясь лишь на свой личный опыт, обусловленный собственными представлениями, догадками, предположениями. Учитывались, тем не менее, небольшие объемы статистических данных, сбор которых, во-первых, был ограничен физическими возможностями человека, ручными методиками, и, во-вторых, представлял собой набор постоянно устаревающей информации, которая просто не могла оставаться актуальной в силу продолжительности процессов сбора, обработки, анализа и доведения до нуждающихся в ней специалистов. С появлением компьютерных технологий человечеству стало доступно формирование весьма приближенных к действительности моделей самых сложных систем, даже таких как «искусственный интеллект» или город.
Несмотря на завораживающее количество перспектив и возможностей, которые открывают перед нами анализ больших массивов данных, современные методики спутниковой съемки или технология «интернета вещей» и по сей день не преодолен скептицизм по отношению к возможностям концептуальной формализации и расчета города. Эта тема, даже с учетом значительного количество попыток «посчитать» город, все еще является малоизученной и слабо структурированной. В большинстве своем профессиональное сообщество продолжает придерживаться традиционных градостроительных и архитектурных методик, с опаской относясь к нововведениям и имплементации новых информационных технологий. Однако эти предубеждения, несомненно, должны быть преодолены, а новые возможности аккуратно и тактично внедрены в сформировавшуюся методику проектирования, поскольку технологии не только ускоряют процесс проектирования и согласования проектных решений, но также вносят недоступную до сих пор для архитектора-градостроителя объективность и фактическую обоснованность принимаемых решений.
Данная статья призвана отчасти структурировать отечественный и зарубежный опыт в теории и практике расчета городских моделей, основанных на точном проективном и функциональном анализе фрагментарных составляющих потенциального континуума города. Параллельно предпринимается попытка выявления ниши в инструментарии архитектора-градостроителя, которую по праву смогут занять современные методики и императивы формирования исчисляемой модели городского пространства.
Генезис классификации моделей «исчисляемого города» в историческом ракурсе градостроительной теории и практики
Согласно классификации, косвенно упоминаемой в книге «Мир архитектуры: лицо города» В. Глазычевым и А. Гутновым [2], модели «исчисляемого города» можно разделить на две группы: «большие» модели и «малые» модели. Основное отличие между ними заключается в том, что «большие» модели служат прогностическим задачам определения наиболее вероятного количественного изменения того или иного городского процесса. «Малые» же модели используются для определения самого оптимального решения из ряда возможных или рассматриваемых.
«Большие» модели
Гравитационная и энтропийная модели используются в прогностических целях для определения наиболее вероятностного массового поведения жителей города. И тот и другой подходы основаны на заимствовании основных положений из физики (термодинамики и теории гравитации).
Гравитационная модель Рейли, описывающая «закон притяжения» между городами, была впервые описана Уильямом Джоном Рейли в его работе «The law of retail gravitation» («Закон розничной гравитации») в 1931 году. В начале книги Рейли ссылается на список из 132 городов США, исследуемых им с 1927 года. В этом списке указаны как большие города («larger cities»), так и малые («smaller cities and towns») [11, с.4]. Рейли приходит к заключению, что большие города, как правило, обладают наибольшим гравитационным притяжением в плане розничной торговли по отношению к малым. Этот постулат лежит в основе всего его дальнейшего рассуждения на тему гравитации городов.
Также Рейли формулирует «Два простых правила», которые описывают поток продаж между городами:
объем продаж города среди жителей других городов растет пропорционально росту численности населения этого города;
город продает больше жителям тех небольших городов, что расположены рядом, нежели тех, что находятся далеко.
На основе этих двух незамысловатых правил формируется идея «точки безразличия» (рис. 1) – точки, лежащей на пути между двумя городами различного «притяжения», откуда покупатель с одинаковой вероятностью может поехать как в один, так и в другой город. Положение этой точки предлагается рассчитывать по следующей формуле:
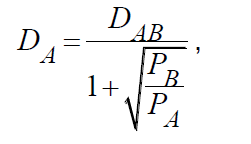
где DA – расстояние от города А до точки безразличия; DAB – расстояние между городами А и В; PA – площадь торгового объекта города А; PB – площадь торгового объекта города В.

Рис. 1. «Точка безразличия» по Рейли
Согласно этой формуле ключевым фактором, влияющим на «притягательность» города, становится площадь его торговых объектов. Примечательно, что «притяжение» городов обратно пропорционально квадратному корню из их торговой площади.
Основываясь на данных положениях, Рейли сформулировал свой закон по аналогии с законом всемирного тяготения Ньютона: «Притяжение Aij, создаваемое городом i в точке j, пропорционально численности населения города Pi и обратно квадрату расстояния D2 , где K – это эмпирически определяемая постоянная» [5].
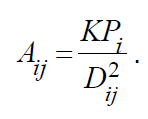
А. Гутнов и В. Глазычев формулируют действие гравитационного закона следующим образом: «корреспонденция между двумя любыми территориальными элементами тем больше, чем больше их условные “веса” (показатели интенсивности их использования) и чем меньше расстояния между ними» [2]. В последствии данный закон множество раз применялся для самых различных расчетов во многих странах, обретая новые формы. В зависимости от стоящей задачи вместо численности населения города могут быть использованы другие показатели, характеризующие исследуемую область. Также подвижен и показатель доступности, а именно: степень, в которую возводится расстояние до исследуемой точки, она может варьироваться в зависимости от ряда факторов, препятствующих или улучшающих доступность.
На основе формулы (2) может быть составлен расчет маятниковой трудовой миграции или притягательности города по любому его признаку:

где транспортная доступность территории характеризуется параметром y, а расстояние D может быть заменено любым другим показателем: временем в пути, стоимостью проезда и других издержек.
Однако закон Рейли имеет ряд недостатков и допущений, сказывающихся на его объективности и точности расчетов. Прежде всего, это его аксиологическая ориентация на капитализм: закон Рейли сформирован мировоззрением общества потребления и сориентирован на торговые характеристики городов как на основополагающие в выборе человеком места назначения. Рейли исходит из предположения, что потребитель равнодушен к любым характеристикам места (к качеству городской среды, к сопутствующим торговле функциям и к наличию специфических товаров и услуг), за исключением общей торговой площади объекта.
Рейли часто необоснованно упрекают за слишком абстрактный подход, однако в конце своей книги «The law of retail gravitation» автор перечисляет ряд факторов, которые могут сказаться на транспортной доступности объектов [11, с.73– 75]. Он упоминает бизнес– привлекательность городов, классы покупателей, топографические и климатические особенности территории и даже газеты и радиообъявления, распространенные на той или иной территории. Все эти параметры невозможно заложить в одну формулу. Этот перечень представляет своего рода пространство для размышлений и анализа в каждом конкретном исследовании.
При всей своей абстрактности и мировоззренческой узости мышления аналогия, проведенная Уильямом Джоном Рейли между ходом взаимодействия пространственных объектов второй природы и законом всемирного тяготения Исаака Ньютона, – это знаковый и переломный момент в формировании концепции «исчисляемого города».
Энтропийная модель пришла на смену гравитационной модели, которая многими была воспринята как эталон прогнозирования межгородского взаимодействия не только в плане торговых взаимоотношений, но и многих других, подводимых под категорию «вес». На смену пришел энтропийный концептуальный подход, позаимствовавший принципы действия у термодинамики.
Энтропийная модель ставит перед собой задачу учета влияния всего многообразия факторов, оставленных вне поля зрения гравитационной теории. По результатам энтропийных вычислений мы получаем не формулу, равно действующую во всех возможных ситуациях, а матрицу возможных вариантов развития событий3. Иными словами, энтропийная модель отвечает более гибкой картине мира, где многообразие возможных вариантов развития событий просчитывается методом «балансировки неувязок». Максимальный разброс возможных решений устанавливается в границах обозначенных ограничений и на основе некоторого стабильного коэффициента. К примеру, в случае расчета трудовых миграций эмпирическим путем было выявлено, что коэффициент y обладает уникальной стабильностью. Данный коэффициент отражает средние для исследуемого района временны́ е затраты на передвижение до места работы (в одну сторону в течение 40 минут [5]). Примечательно, что этот параметр, называемый «бюджет времени работающего населения», остается весьма стабильным в условиях практически любых изменений системы: роста агломерации, изменении ценовой политики на транспортные услуги или колебания количества рабочих мест. Представляется весьма интересным тот факт, что стабильность данного показателя приводит нас не только к прогнозу миграции трудового населения, но и к решению вопроса планирования жилищного строительства, спрос на который также определяется временны́ ми затратами на дорогу до места работы.
3 Приводить набор формул, характеризующих расчет в случае энтропийной модели, видится малоэффективной практикой, поскольку, в отличие от гравитационной модели, расчеты в каждом конкретном случае имеют довольно уникальный вид и не раскрывают более наглядно предложенный метод, нежели это может быть сделано в текстовой форме.
В противоположность статичной гравитационной, энтропийная модель отличается широкими возможностями расширения и усложнения, связанными с добавлением в нее вероятностных передвижений населения, не занятого в трудовой деятельности, а также передвижений по ряду других причин – рекреация, покупки, получение услуг.
Основная задача в градостроительной практике, которая решается с помощью расчета энтропийных моделей, – это формирование схем территориального планирования. Для получения более целостной картины в этом случае могут применяться расчеты по отдельным группам населения и видам транспорта.
Энтропийный подход использовался для расчета обоснования транспортных решений Генерального плана Ленинграда и Ленинградской области в 1987 году, а также Генерального плана Санкт-Петербурга 2005 года.
Транспортную модель, представляющую собой комбинацию энтропийного и гравитационного подходов, выделять в отдельную категорию не имело бы смысла, если бы она наилучшим образом не демонстрировала недостатки и «белые пятна» «больших» моделей. Пытаясь решить транспортную проблематику конца XX века, ученые, экономисты и градостроители столкнулись с несоответствием между расчётными, предполагаемыми результатами и фактическими эффектами, которые вызывают попытки просчитать и скорректировать систему.
Парадокс Доунса-Томсона. В 1960-х годах Э. Доунс [8] и Дж.М. Томсон выявили парадокс, суть которого сводится к тому, что в районах, где в час-пик наибольшая нагрузка по передвижению населения приходится на общественные виды транспорта (метро, выделенные полосы для автобусов и такси), при увеличении пропускной способности дорог часть населения пересаживается с общественного транспорта на индивидуальный автомобиль, и, таким образом, восполняет любой возникший люфт пропускной способности улично-дорожной сети (УДС). Здесь мы сталкиваемся с «идолом пещеры» английского философа-материалиста Френсиса Бэкона: индивидуальное заблуждение каждого участника дорожного движения, рассчитывающего сократить свой путь, приводит к общему снижению скорости транспортного потока и сводит к нулю любые улучшения, произошедшие в УДС, в том числе на основании гравитационных и энтропийных расчетов.
Примечательно, что парадокс Доунса-Томпсона может не только свести к нулю положительный эффект модернизации УДС, но и даже привести к обратным результатам. Снижение спроса на общественный транспорт влечет за собой удорожание тарифов, что в очередной раз мотивирует население пересаживаться на индивидуальный транспорт и влечет за собой еще большие заторы, нежели те, которые пытались скорректировать расчетом и модернизацией.
Постулат Льюиса-Могриджа. «Закон неминуемой перегрузки», сформулированный Доунсом, нашел свое отражение в постулате Льюиса-Могриджа (1990 г.), который гласит, что сколько бы ни строилось дорог, всегда образуется нужное количество транспорта, чтобы заполнить их [10]. Известие о преимуществах новых дорог непременно приводит на них новых автомобилистов, что в довольно короткие сроки нивелирует все преимущества от нововведений. Тут мы сталкиваемся с «идолом площади» Ф. Бэкона: СМИ, транслирующие информацию о новых участках дороги и развязках, специальные приложения, прокладывающие оптимальные маршруты через новые участки УДС, – вся эта система, призванная облегчить ситуацию на дорогах, приводит к неверному толкованию произошедших изменений и создает неоправданную нагрузку и заторы уже на новых участках УДС.
Парадокс Браеса. В 1968 году, немецким математиком Дитрихом Браерсом был открыт парадокс, который гласит: добавление элементов в систему, в том числе строительство новых альтернативных объездов, при условии, что движущиеся по системе объекты (автомобилисты) сами выбирают свой путь, может привести к ухудшению ситуации во всей транспортной сети, поскольку приводит к увеличению пути по всем маршрутам. Таким образом, несмотря на очевидную эффективность мер по расширению УДС на основе традиционных расчетов, на практике существует высокая степень вероятности достижения наибольшей эффективности работы системы обратным действием, т.е. сокращением УДС. Наглядным тому примером может служить ситуация в Штутгарте (Германия), где дорожный поток так и не смог стабилизироваться после инвестиций в строительство УДС 1969 года пока часть новой дороги не была закрыта для проезда [9].
Рассуждая о «больших» моделях города следует обратить внимание на репрезентативность трех вышеобозначенных транспортных парадоксов – они отображают несостоятельность прогностических моделей, по крайней мере, в их первоначальной концептуальной формулировке. Вопрос формирования модели, охватывающей если не все, то большинство аспектов города как пространственной, социальной, экономической единицы, остается открытым и актуальным, особенно в современных условиях глобализации, устойчивого экологического подхода и формирования четвертой промышленной (цифровой) революции. Для того, чтобы рассмотреть и другие возможные подходы к «оценке» города, перейдем к анализу «малых» моделей.
«Малые» модели (оценочные)
В отличие от «больших» моделей, которые наделяются прогностической функцией, «малые» модели используются для оценки существующего потенциала территории по тому или иному параметру, а также для рассмотрения и принятия решения при выборе из нескольких предложенных проектов, сформированных традиционными методами.
Демографический потенциал, как пишут Гутнов и Глазычев, это «показатель числа возможностей, которыми располагает житель данного района города при осуществлении той или иной деятельности» [2], иными словами, демографический потенциал в той или иной мере косвенно выражает «спрос» на территорию. Потенциал территории может быть оценен и улучшен по ряду параметров, в том числе:
УДС и доступность территории;
места приложения труда;
места досуга;
социальная инфраструктура;
благоустроенность общественных пространств;
уникальность среды.
Улучшение комплекса параметров демографического потенциала территории или же оценка и развитие хотя бы одного из них непосредственно влияют на спрос и стоимость
данной территории – как ментальную, так и фактическую, материальную. Особенно важным представляется переход от демографических показателей «обеспеченности» территории, обширно отраженной как в нормативной базе, так и в градостроительной документации, к ее экономической оценке. Происходит своего рода смена социалистической парадигмы, ее симбиоз с капиталистическими эффективными методами управления развитием территорий.
Стоимостной подход – это логическое продолжение системы оценки демографического потенциала, поскольку включение территории в экономическую систему отношений города представляется наиболее эффективным способом проявления всего практического потенциал «оценочных» методов. Результатом применения этого метода «исчисления» города становится кадастр его территорий, дающий оценку экономической эффективности и привлекательности каждого отдельного участка и/или объекта, а, следовательно, являющийся отправной точкой для разработки как общей стратегии развития территории в целом, так и принятия решений по отдельным ее частям.
«Оценочные» модели, несмотря на свою эффективную помощь в принятии оптимальных решений как проектировщиком, так и городскими властями, имеют ряд недостатков и сопровождающих сложностей. Не представляется удивительным тот факт, что «оценочные» методы не имеют готовых формул или наборов параметров, по которым должна быть проведена оценка той или иной территории, однако общий принцип предельно ясен. В каждом конкретном случае определяется оценочная шкала и набор параметров, на нее влияющий, а у каждой территориальной единицы тем или иным способом вычисляется ее «генерирующая» и «поглощающая» способность.
Прежде всего, это вопрос формализации данных, необходимых для проведения оценки, то есть их «перевод» на машинный язык. Здесь мы сталкиваемся с одним из наиболее весомых ограничений «подсчета» города – большая часть градостроительной проблематики не поддается формализации, что подводит нас к вопросу о возможности или, скорее, невозможности создания «электронного градостроителя».
Следующая проблема, не менее важная, – объективность списка рассматриваемых и оцениваемых параметров. Как определить необходимый минимум для достижения объективности оценки и в то же время не усложнить систему расчетов до состояния невыполнимого? Как интерпретировать и верифицировать полученные результаты, определить эффективность действия системы со временем? Как предугадать наличие парадоксов, разрушающих стройную логику системы? Как их в нее включить? На эти и многие другие вопросы архитектору-градостроителю лишь предстоит ответить.
Рассмотрев типологию концептуальных подходов к созданию модели города, можно сказать, что их деление, предложенное в книге «Мир архитектуры. Лицо города» [8], на «большие» и «малые» следовало бы трактовать как деление на «прогностические» и «оценочные» по типу получаемого вывода (результата). Примечательно, что также два этих подхода отражают и два мировоззренческих выбора: чему отдается приоритет в принятии конечных, итоговых решений – математическому расчету (компьютерным вычислительным технологиям) или же человеку (архитектору-градостроителю)? Косвенным образом, классификация концептуальных подходов по формированию модели города ставит вопрос о конечной цели развития данного раздела градостроительной и экономико-географической наук: стремимся ли мы создать «электронного градостроителя» или вложить новый мощный вычислительный инструмент в готовальню специалиста? На сегодняшний день все же приоритетным и наиболее реалистичным видится второй вариант.
Проанализируем вероятностную степень реализации вышеобозначенных концепций в градостроительной теории и практике.
Научно-прикладная значимость концептуальных градостроительных императивов в конституировании современного городского пространства
Основываясь на методах индустриальной динамики, разрабатываемых с 1956 года профессором Массачусетского технологического института – Альбертом Слоуном, Дж. Форрестер предлагает свое виденье подхода к построению модели города в книге «Динамика развития города» [6]. Форрестер сравнивает город с другими сложными системами, развитие которых обуславливается обратной связью – положительной и отрицательной. К таким «подвижным системам» он относит философские, промышленные, экологические, биологические и социальные. По мнению Форрестера, применение методов индустриальной динамики к городу позволяет перевести его на язык ЭВМ и проследить возможные модификации поведения системы урбанизированных территорий на основе имитации изменения руководящих причин.
Конкурентным преимуществом данного подхода относительно других является то, что город Форрестер рассматривает как саморегулирующийся, устойчивый организм подобный живому своей «непредсказуемостью» и «нечувствительностью» даже к самым сильным изменениям его ключевых параметров [2]. Поэтому, несмотря на сугубо математические методы расчета системы, она представляет собой более гибкий подход, учитывающий возможные изменения и «вторжения извне» в устоявшуюся и стабильную картину мира.
Описанная модель динамического развития применима к городу с момента установления в нем «равновесного состояния», которое достигается к концу цикла роста. Прогноз, составленный на основе модели Форрестера, покрывает ближайшие 50 лет развития урбанизированной территории и показывает не только возможные варианты ее развития, но также демонстрирует на ряде примеров несостоятельность предлагаемых и применяемых программ развития города [6, с.14]. Так, например, программы по обеспечению не полностью занятой категории населения дешевым жильем, вопреки ожиданиям, вели исключительно к стагнации затрагиваемых систем, а не к их развитию [6, с.76-81].
Предваряя энтузиазм в управленческих структурах по поводу применения данной системы, Форрестер акцентирует внимание на том, что предлагаемая им модель города имеет ряд допущений, и, следовательно, для достижения удобоваримой объективности должна корректироваться для каждого конкретного случая. Имитационная модель Форрестера предполагает следующие 3 допущения:
Специфика территории. Одним из важнейших ограничений имитационной модели является ее максимальный возможный территориальный обхват. Это не город в его административных границах, а какая-то его часть, к примеру – центр или пригородный район. Рассматриваемая территория должна быть достаточно малой для того, чтобы в ее границах могли устанавливаться экономические и культурные взаимосвязи между различными категориями населения, из которых выделяются три категории «подвижного» населения, способного мигрировать «в» и «из» города: «менеджеры-профессионалы, неполностью занятые и занятые» [6, с.14].
Неисчерпаемость окружающей среды. Второе допущение предусматривает, что окружающая среда изучаемой социальной системы – города или его фрагмента – рассматривается как неисчерпаемый ресурс, способный предоставлять население в необходимых количествах и в течение любого времени до тех пор, пока город является сравнительно привлекательным по отношению к окружающей его среде. Таким образом, окружающая среда выступает в роли исходных данных, на основе которых решается задача о миграции населения и динамике занятости.
Относительная притягательность. Притягательность городской территории по Форрестеру – это изменяемый показатель, зависящий прежде всего от внешних, не
поддающихся влиянию факторов притягательности окружающей среды, и внутренних изменяемых факторов, связанных с условиями и деятельностью внутри города.
К компонентам притягательности Форрестер относит:
состояние жилого фонда;
характер работы;
объем коммунальных услуг;
юридические ограничения;
предубеждения;
расовые и этнические группировки;
традиции.
Следует отметить, что при этом спектр осознанного влияния на компоненты привлекательности города не слишком широк. С одной стороны, он ограничен взаимосвязанностью факторов, когда рост одного ведет к снижению другого, с другой, – тягой города к уравновешенности.
На основе данных трех допущений, можно сформулировать «закон равновесия», согласно которому миграция населения в городе как стабильной системе происходит до тех пор, пока изменение ряда факторов не ведет к установлению равновесия между степенью привлекательности урбанизированной территории и окружающей ее среды.
Но при всей объективности данного закона из него имманентно проистекает и главный недостаток модели Форрестера. Приводимая в книге «модель 250-летнего развития города», предлагаемая как усредненная динамика достижения равновесного состояния города, опирается на сугубо специфические условия, характерные конкретно для США, например: снижение квартирной платы в зависимости от обветшания жилого фонда и, как результат этого, уплотнение стагнирующих районов за счет заселения их малоимущими жителями, или размещение новых сфер бизнеса вне городской черты в связи с устареванием нежилого фонда. Такое «равновесное состояние» нетипично для многих других городов, а значит, и применимость модели весьма ограничена и изначально требует подробного уникального перерасчета основных ограничивающих факторов.
Преимущество модели Форрестера состоит в том, что исследователь на ряде примеров проиллюстрировал несостоятельность изначально положительных мер по улучшению городского состояния. Аналитически было доказано, что такие программы, как занятость, профессиональное обучение не полностью занятых, субсидирование из федерального или регионального бюджета и строительство дешевого жилья устойчиво коррелируют с тремя парадоксами транспортной модели [6]. Таким образом, имитационная модель Форрестера демонстрирует свое основное преимущество над другими моделями, поскольку она включает в себя всю «парадоксальность» провала интуитивно понятных решений и демонстрирует основное свое назначение – проверку краткосрочных и, что самое главное, долгосрочных управленческих решений на их эффективность в будущем – оценочно-прогностическую задачу как новую категорию в рассмотренной изначально классификации «больших и малых» моделей.
Уникальность практического имитационного подхода Форрестера заключается в том, что, в отличие от вышеобозначенных «больших» и «малых» моделей, данная концепция тяготеет не к «сложности» Колмогорова [1], трактуемой в качестве меры вычислительного ресурса, необходимого для точного определения объекта – «длины сжатого файла», а «сложностности»4, философски понимаемой и объясняемой как «наблюдение наблюдателя».
4 Понятие, введенное Аршиновым В.И. в его работе Сложностный мир и его наблюдатель. Часть первая / В.И. Аршинов, Я.И. Свирский // Философия науки и техники. – 2015. – Т. 20. – № 2. – С. 70–84.
Аксиологическая характеристика структурно-функционального потенциала Москвы и Ленинграда в 1980-е годы
В 1980-е годы, на основе оценочных подходов к расчету потенциала города, была проведена характеристика структурно-функционального потенциала Москвы и Ленинграда. Структурно-функциональный потенциал – это показатель, измеряемый в условных единицах и позволяющий дать обобщенную оценку всему городу и выявить в нем максимально привлекательные для жителей «точки» урбанизированной территории.
Согласно анализу, проведенному в 1980-е годы, для оценки территорий Москвы удалось выяснить, что наибольшая привлекательность – порядка 80% – приходится на всего лишь 10% территории города. Особого внимания заслуживает метод визуализации полученных результатов – преобразование плохо читаемых числовых показателей в наглядную карту «пиков», составляющих каркас городской территории. На основе данного анализа было сделано следующее заключение: размещение новых объектов городского значения в центре города даст больший прирост (около 40%) по сравнению с возможным приростом потенциала системы в 10% при развитии периферийных центров, как это задумывалось генпланом 1971 г.
Верификация методом социального опроса. Особо важен для понимания эффективности системы был проведенный сравнительный анализ между полученными расчетными показателями модели и опросом жителей о наиболее привлекательных местах тогда еще Ленинграда, ныне Санкт-Петербурга. В большинстве своем результаты совпали, подтверждая эффективность метода, однако особого внимания заслуживали пики «несовпадений», пришедшиеся на набережные реки Невы в районе Стрелки и центральные части города, с аналитической точки зрения не блещущие функциональным разнообразием и потенциалом, но, тем не менее, пользующиеся большой популярностью у населения.
Стоит обратить внимание на то, что данные несоответствия ни в коей мере не скомпрометировали математическую часть расчетов, лишь только продемонстрировали очевидную слабость «оценочных» моделей – узость охвата. Очевидно, что при функциональном подходе в данном случае были упущены вопросы эстетических качеств городской среды, традиционности, «духа» места, «центральности» и многие другие.
Несмотря на столь выразительный опыт, демонстрирующий как слабость использования только лишь расчетной модели, так и значимость мнения жителей, выраженного в данном случае в виде опроса, в отечественной практике так и не предложено комбинированной системы оценки потенциала города, которая бы включала как математический подход (любой из обозначенных выше или их комбинацию), так и мнение непосредственного реципиента всей деятельности – горожанина.
Суммируя вышесказанное, можно сделать следующие выводы:
На основе проведенного анализа, несомненно, не претендующего на полную объективность и всеобъемлющий охват, можно предложить классификацию концептуальных подходов к построению и расчету модели города (таблица 1).
Предложенная классификация может пополняться новыми типологиями, но, что более интересно, может быть рассмотрена в ключе двух математических парадигм: теории хаоса и теории поля как противопоставляемых подходов к созданию модели.
Несмотря на значительные различия в математических подходах и в формате конечного результата, все описанные модели имеют общее «белое пятно» – отсутствие связи с мнением горожанина, непосредственно реципиента градостроительной деятельности.
Интегральное оптимальное решение, скорее всего, лежит в кумулятивном подходе, то есть применении комплекса методов формирования городской модели в комплекте с социологическими опросами и современными техниками сбора и анализа больших данных о городе, работе его систем и поведенческом факторе его жителей.
Таблица 1. Классификация подходов к расчету модели города
Охват | Большие модели | Малые модели | |||
Характер | Прогностические | Оценочно-прогностические | Оценочные | ||
Название | Гравитационная модель | Энтропийная модель | Имитационная модель | Демографический потенциал | Стоимостной подход |
Автор | Рейли | — | Форрестер | — | — |
Представленное исследование не охватывает всего возможного спектра существующих концепций «исчисляемого города», всей проблематики этой темы и возможностей ее применения. Но в результате его становится очевидным тот факт, что тема «исчисляемого города» имеет очень важное значение для развития современной градостроительной практики и должна быть как можно более подробно изучена и развита в дальнейших научных, исследовательских и практических работах.
Литература
Верещагин Н.К. Колмогоровская сложность и алгоритмическая случайность / Н.К. Верещагин, В.А. Успенский, А. Шень. – М.: МЦНМО, 2013. – 576 с.
Гутнов А.Э. Можно ли «сосчитать» город? / А.Э. Гутнов, В.Л. Глазычев // Мир архитектуры. Лицо города. – М.: Молодая гвардия, 1990.
Гутнов А.Э. Структурно-функциональный анализ градостроительных систем с использованием количественных характеристик (на примере г. Москвы) // Города и системы расселения №3: Достижения и перспективы. – Выпуск 18, 1981. – С. 43-51.
Есаулов Г.В. От «умного города» к «умной» системе расселения // Сборник Современная архитектура мира. – Выпуск 5. – М., СПб, 2015. – С. 9-20.
Региональная экономика и пространственное развитие. В 2 т. Т. 1. Региональная экономика. Теория, модели и методы : учебник для бакалавриата и магистратуры / под общ. ред. Л. Э. Лимонова. – М.: Издательство Юрайт, 2014. – 397 с.
Форрестер Дж. Динамика развития города. – М.: Прогресс, 1974. – 287 с.
Шваб Т. Четвертая промышленная революция. – М.: «Эксмо», 2016. – 138 с.
Downs A. Stuck in Traffic: Coping with Peak-Hour Traffic Congestion. – Washington (DC): The Brookings Institution. – 1992. – 210 s.
Knödel W. Graphentheoretische Methoden Und Ihre Anwendungen. – Vienna: Springer– Verlag. – 1969. – S. 57–59.
Mogridge M.J.H. Travel in towns: jam yesterday, jam today and jam tomorrow? – London: Macmillan Press, 1990. – 308 s.
Reilly W.J. The law of retail gravitation // 285 Madison Avenue New York. – 1931. – 75 p.