Философско-геометрические системы мер длины храмостроения Древней Руси X–XV веков

М. Э. Венгерова

Московский архитектурный институт (государственная академия), Москва, Россия

Аннотация

В статье проводится анализ взаимосвязи мер длины, использовавшихся в храмостроении Древней Руси, с ранее выявленными геометрическими закономерностями построения пропорций храмов, тесно связанных с христианским пониманием мироустройства. В размерении интерьеров древнерусских храмов X-XV веков было обнаружено: применение задачи «квадратура круга», по которой выстраивались габариты церквей с пропорциями 8:9, 10:13, 2:3, 5:8; наличие «Животворящего столпа» в центре подкупольного квадрата, горизонтальная проекция которого равна по площади подкупольному квадрату в ¾ храмов, а высота до центральной точки свода кратна его диаметру в соотношениях 1:3, 1:4, 1:5. Выявлены геометрическая запись богословского образа св. Троицы, находящаяся по ширине структурного ядра храма в виде горизонтальной проекции «реки» божественного света, льющегося из подкупольного пространства и разделяющегося на два рукава, и символические дробные членения, использовавшиеся при практическом размерении смысловых зон «мира видимого» и «невидимого». Предлагается восстановление летописного названия меры Пояс Христа (1,05-1,08 м), представляющего собой половину византийской сажени оргии (2,12-2,17 м). Объясняется разница двух вариантов упоминания в древнерусских храмах св. Троицы, как богословского понятия через геометрическо-символический начертанный образ или, как посвящения ей: «во имя Отца и Сына и Св. Духа».

Постановка вопроса о философско-геометрическом анализе мер длины, применявшихся в древнерусском храмостроении

В нашей предыдущей научно-исследовательской работе «Геометрическое пропорционирование древнерусских храмов X-XV веков» [1, 2, 3] было сделано несколько находок, которые интересны для дальнейшего изучения всей системы размерения христианских храмов на местности. Была выявлена запись богословских понятий через геометрические схемы, обнаруживающиеся в анализе пропорций церквей и соборов: св. Троицы – это три круга, центры которых находятся на одной прямой на расстоянии радиуса друг от друга (рис. 1а, б), как горизонтальной проекции образа, описанного святителем Григорием Богословом (IV в.), в виде реки света, льющейся с небес и у земли разделяющейся на два рукава, что и визуализируется в храме, где свет из окон барабана льётся от изображения Христа на центральном своде, заполняя ниже всю ширину трёх центральных нефов; «небо на земле», как геометрические решения задачи «квадратура круга» (рис. 1в, г) и совмещение этих двух схем при размерении внутренней ширины трёх центральных нефов и подкупольного квадрата. Найдена последовательная запись христианского мировоззрения: что было в начале – это Бог, он был всегда, его символ круг, и именно он вначале размерялся под архитектурной доминантой в центре храма как горизонтальная проекция «Животворящего столпа», в образ Церкви как Башни [4, c.297] на месте встречи с Богом – его Вознесения, ибо сказано: «Сей Иисус, вознёсшийся от вас на небо, придёт таким же образом, как вы видели Его восходящим на небо» (Деян. 1:9-11).

После была создана земля, её символ – квадрат, и их два в храме: подкупольный и габаритный, сторона второго равна внутренней ширине трёх центральных нефов. Относительно этого большего квадрата размерялся Престол, как символ либо Гроба Господня, и тогда весь Престол находился на территории символического квадрата земли, либо Трона Царя мира, тогда центр престола находился на восточной стороне квадрата храма, чтобы Трон располагался «как на небе, так и на земле» [2]. Геометрические схемы подтвердили нахождение символического «видимого неба» перед иконостасом, а «неба невидимого» – за ним, граница же между мирами – иконостас с иконами находится ровно посередине большого круга, равного по площади квадрату храма со стороной, равной внутренней ширине трёх центральных нефов [1].

а) б) в) г)

Условные обозначения: A – сторона квадрата, равного по площади кругу; D – диаметр круга, равного квадрату по площади; R – радиус круга, равного квадрату по площади; O – центр серединного круга; O’, O’’ – центры двух дополнительных кругов, равных центральному, строящиеся для получения точек пересечения окружностей, расстояние между которыми, являясь отрезками MN и M’N’, равно стороне квадрата, равного по площади кругу; Ш – ширина ядра храма в интерьере, равная внутренней габаритной ширине трёх центральных нефов.

Рис. 1. Геометрические записи богословских понятий и последовательности размерения, использовавшиеся в древнерусском храмостроении X-XV вв.: а) «Животворящий столп» – дом Бога на земле; б) Богословский образ св. Троицы, как горизонтальная проекция

«реки» по Григорию Богослову; в) «небо на земле», как решение задачи «квадратура круга»; г) геометрическое построение внутренней ширины трёх центральных нефов и подкупольного квадрата

Известно, что древние строители пользовались как антропоморфными мерами человеческого тела (сажени, локти, шаги, стопы, пяди и т.д.), так и священными для Христианства, например – золотой Пояс Христа, которым Богородица, явившаяся строителям, велела размерить основные габариты собора Успения Пресвятой Богородицы в Киево-Печёрском монастыре (1073 г.).³ Так же известны случаи хранения Поясов в размер Гроба Господня, например, в алтаре собора св. Софии в Новгороде [5]. Поэтому в продолжение ранее начатого исследования было интересно найти взаимосвязь между уже найденным геометрическим размерением древнерусских храмов X-XV веков с мерами длины, использовавшимися во времена строительства исследуемых памятников. Гипотезой нашего дальнейшего исследования является предположение существования таких систем взаимосвязи мер длины, которые помогали решать геометрические задачи ещё более простыми способами и имели бы богословский символический смысл, важный для христианского миропонимания.

3 Киево-Печёрский Патерик, или сказания о жизни и подвигах Святых Угодников Киево-Печерской Лавры. – Киев: Лыбидь, 1991. – 256 c.

Геометрическая теория взаимосвязи древнерусских мер длины

Ввиду того, как писал Роберт Оделл Борк [6] на примере описываемых им чертежей для готических соборов, что, если есть какой либо алгоритм в строительстве, то он с наибольшей вероятностью проявляется на всех стадиях от решения большого объёма до деталей. Поэтому первыми задачами, которые были поставлены, был поиск взаимосвязи древнерусских мер длины, использовавшихся в храмостроении, с геометрическими решениями задачи «квадратура круга», геометрическим изображением богословского догмата Святой Троицы и встречающегося использования дробей при практических размерениях функциональных зон за счёт простого деления шнура и взятия его частей, которыми измеряются в символической цепи последовательности пространства в храме.

Анализ древнерусских мер длины с точки зрения решения геометрических задач был начат академиком Рыбаковым Б.А. ещё в 1949 году.⁴ Эта идея развивалась и далее. Такой подход, с точки зрения утилитарного использования саженей, раскрывает методы зодчих, используемые на строительной площадке, так как невозможно размерить прямоугольный план шнуром без диагонали, иначе получится ромб. Эту проблему решали ещё в Древнем Египте. Ранее учёные анализировали, как парные меры, использовавшиеся для построения квадратов, такие как простая и косая сажени, то есть сторона и диагональ квадрата, так и дробные деления целых саженей, могут создавать систему универсальных членений, удобных для практического применения и возможности решения различных задач вычисления площади и объёма. Например, построение прямого угла треугольником со сторонами 3 и 4 частей, а диагональю 5 (Афанасьев, 1954, 2002⁵), или, как писал Бондаренко И.А., квадрат со стороной 5 имеет диагональ 7 стоп (Бондаренко, 1988⁶). Сажени систематизировались так же Афанасьевым К.Н. Рыбаковым Б.А. (1957⁷, 1974⁸), Пилецким А.А. (1980^9,10), Шевелёвым И.Ш. (1963¹¹, 2009¹²), Бондаренко И.А. (1988), Радзюкевичем А.В. (1989¹³), Черняевым А.Ф.¹⁴ (1998), Черновым А.Ю. (2006¹⁵), Павловым Н.Л. (2018¹⁶) и другими в поисках различных практических объяснений существовавшему разнообразию.

4 Рыбаков Б.А. Русские системы мер длины XI-XV веков // Советская этнография. – 1949. – № 1. – С. 67-91.

5 Афанасьев К.Н. Построение архитектурной формы древнерусскими зодчими. – М.: Ладомир, 2002. – 276 с.

6 Бондаренко И.А. К вопросу об использовании мер длины в древнерусском зодчестве // Архитектурное наследство: Русская архитектура. – № 36. – М.: Стройиздат, 1988. – С. 54-63.

7 Рыбаков Б.А. Мерило новгородского зодчего XIII века // Памятники культуры. Новые открытия. Письменность. Искусство. Археология. Ежегодник 1974. – М.: Наука, 1975. – С. 205-218: icon-art.info/bibliogr_item.php?id=3784

8 Рыбаков Б.А. Архитектурная математика древнерусских зодчих // Советская археология. – 1957. – № 1. – С. 83-112 : tehne.com/node/1732

9 Пилецкий А.А. Метрологические исследования памятников древнерусской архитектуры // Источники и методы исследования памятников градостроительства и архитектуры. – М., 1980. – С. 112–117.

10 Пилецкий А.А. Система размеров и их отношений в древнерусской архитектуре // Естественнонаучные знания в Древней Руси. – М., 1980. – С. 63–109.

11 Шевелёв И.Ш. Основы гармонии. Визуальные и числовые образы реального мира. – М.: Луч, 2009. –C. 79.

12 Шевелев И.Ш. Геометрическая гармония. Опыт исследования пропорциональности в архитектуре. – Кострома: Обл. типография им. Горького Костромского полиграфиздата, 1963. – C.14, 20.

13 Радзюкевич А.В. Особенности построения храмов Владимиро-Суздальской Руси методом "по образцу". Рукопись депонирована во ВНИИТАГ Госкомархитектуры 17.04.89, – № 764 : rusarch.ru/radzukevich1.htm

14 Черняев А.Ф. Золото Древней Руси. Русская матрица – основа золотых пропорций. – М.: Белые альвы, 1998. – 144 с.

15 Чернов А.Ю. Хроники изнаночного времени. "Слово о полку Игореве": текст и его окрестности. – СПб.: Вита Нова, 2006. – 480 с.

16 Павлов Н.Л. Архитектура. Введение в профессию. – М.: Архитектура-С, 2018. – 472 с.

Коснёмся некоторых систематизаций, которые представляют интерес для нашего исследования. Б.А. Рыбаков пишет о четырёх саженях, «образующих единую геометрическую систему»: мерная (1,76 м), великая (2,49 м), прямая (1,53 м) и косая (2,16 м). И как о части, входящей в эту четвёрку, о тройке саженей: мерная, великая и прямая, применявшихся, по его утверждению, для проверки объёма здания (Рыбаков,1974). Также он описывает «сажень без чети» (1,96 м), называя её мерой «искусственно созданной», являющейся диагональю половины квадрата со стороной равной мерной сажени (1,76 м) и диагональю, равной косой сажени (2,48 м) (Рыбаков, 1957). То есть, для практического размерения планов гражданских зданий на местности вполне хватает прямой и косой саженей, а для пропорционирования церквей появляется ещё дополнительная мера, равная диаметру круга, равного по площади квадрату, который размечают на местности. В ходе нашего предыдущего исследования нашлось богословское объяснение появлению в христианском храмостроительстве именно таких троек мер, как решения задачи «квадратуры круга» [1]. О паре 1,76 м и 2,16 м, Шевелёв И.Ш. пишет как о второй группе мер, «данных человеку самой природой» (Шевелёв, 2009). Пилецкий А.А. говорил, что в древнерусской архитектуре «все измерения были трёхчастными» (Пилецкий, 1980), и объяснение этому он находит в «трёхчастном делении» человеческого тела и «живой природы». Н.Л. Павлов отмечает, что для разметки храмов был свой набор мер, отличавшийся от жилого строительства, также он описывает кратность десяти как антропоморфную, исходящую из количества пальцев, а двенадцати, как применявшуюся для исчисления времени и движения светил по небу.¹⁷

17 Там же, С. 13,18.

Таким образом, предыдущими исследователями выявлялись закономерности, которые в нашем исследовании также учитывались, при этом была добавлена систематизация с точки зрения найденных геометрических схем, задач и дробей, связанных именно с христианским мировоззрением, которые имели практическо-символическое использование в храмостроении Древней Руси X-XV веков [2, 3].

«Квадратура круга», раскрывающая символические взаимосвязи меры длины древнерусского храмостроения

Итак, зная, что квадрату необходима диагональ, а для размерений христианских храмов необходимо символическое построение равных по площади круга и квадрата, можно предположить, что существовали также и тройки мер, тесно связанные с богословским пониманием мироустройства. В подтверждение этого можно привести древнерусский артефакт конца XII века, найденный в 1970 году экспедицией Монгайта в культурном слое XIII века в Новгороде (Рыбаков, 1974; Шевелёв, 2009). Это – центральная часть мерной трости, дошедшей до нас в виде двух обломков четырёхгранного бруска, на три стороны которого нанесены насечки, соотносящиеся между собой последовательно как диагональ квадрата, сторона квадрата и диаметр круга, равного по площади этому квадрату. Рыбаков реконструировал средние размеры насечек на основании анализа двух отдельных частей мерила (22 и 32 см). Количество сохранившихся делений на различных гранях колеблется от трёх до шести. Рыбаков пишет, что неточности разделений колеблются до половины сантиметра, и наблюдаемые «нами средние размеры могут рассматриваться лишь как приближение к истинам» (Рыбаков, 1974), поэтому не стоит впадать в перфекционизм сотых частей от миллиметров, тем более что и фактические строительные методы древнерусского строительства в целом позволяют допускать округления. Если размер одного шестисантиметрового деления принять за сторону квадрата, то ему соответствующая диагональ будет около восьми см, а диаметр круга, равного по площади этому квадрату – около семи см. Факт существования этого «мерила» позволяет утвердиться в нашем предположении о символических «тройках» линейных мер длины, которые существовали именно в христианском храмостроении. Такая система мер, кроме размерения габаритов храмов, могла использоваться для практического удобства изготовления, например, кружал или при разметке декора. Такие закономерности трёх пропорциональных соответствий обнаруживались при анализе пропорций каменных узоров древнерусских храмов, но эта тема должна быть ещё дополнительно изучена.

Далее нами были найдены соответствующие друг другу тройки древнерусских саженей, соотносящиеся между собой как сторона квадрата (а), диагональ этого квадрата (с) и диаметр круга (д), равного по площади этому квадрату. Например, из часто встречающихся мер, это: 1,55 м (а), 1, 74 м (д) и 2,17 (с). Триада может быть описана и другой «цепочкой» соответствий: 2,17 (а) – 2,44 (д) – 3,05 (с). Также нами были выявлены меры при анализе размеров центральных подкупольных квадратов в планах церквей: Рождества Богородицы в Перыни (1230–1240 гг.) 2,44 м – 2,84 м – 2×1,75 м [7]; собора Успения Пресвятой Богородицы во Владимире (1158–1161 гг.) 2×3,25 или (3×1,08 м) – 3×1,22 м (полсажени от Великой 2,44 м) – 3×1,52 м [8]; Преображения Спаса на Нередице (1198 г.), такая же, как предыдущая, система исходит из меры в 1,07 м [9]; в соборе Святой Софии в Новгороде (1045–1052 гг.) 3×2,10 м – 3×2,49 м – 3×2,84 м [10]; в Николо– Дворищенском соборе (1113 г.) 2×2,49 м – 2×2,84 м – 4×1,75 м [11]. И таких цепочек можно построить множество для различных храмов, некоторые будут иметь в основе одни и те же меры, но взятые разное количество раз в зависимости от размеров сооружения. Представленные цепочки дают возможность понять некоторую взаимосвязь мер в древнерусском храмостроении, объединяя этот разрозненный набор саженей в стройную систему, связанную с выявленными ранее правилами построения геометрических пропорций планов [1].

Поиск взаимосвязей мер привёл к исследованию малых мер человека, так как «меры же почерпаются из частей человеческого тела» [12, с.50]: аршин, являющийся шагом; локоть; стопа; пядь. Нами была воссоздана схема этих соответствий (рис. 2), которая выявляет некоторые символические результаты, подтверждающие ранее доказанные, о том, что внутренняя длина в храмах строится иррационально из простых геометрических начертаний правила «квадратура круга» [13]. Так, квадрату со стороной равной локтю (0,52–0,54 м), являющимся половиной Пояса Христа (1,05 м), ранее называвшимся Поясом Шимона, вычисленным из размеряемой целыми мерами внутренней ширины Успенской церкви Киево-Печёрского монастыря (1073 г.) (Рыбаков, 1949), будет соответствовать диагональ длиной в один аршин (0,72-0,74 м), то есть шаг; радиус круга, равного этому квадрату по площади, будет равен стопе (0,315 м), а диаметр этого же круга – трём пядям (0,21 м), которые, в свою очередь, равны длине лица человека от подбородка до основания волос. Таким образом, диаметр круга, являющегося в христианстве символом Бога, равен трём лицам, «троелица» – Троице. Как пишет Симеон Солунский: «именем Святой Троицы, провозглашая три Лица в одном Божестве» [14, с.70], так и три распахнутые пяди, как могущие «восприять Царя» [15, с.236], заключены в круг – символ Слова. Так Василий Великий, описывая Слово, что «было в начале», сравнивает его с солнечным кругом.18 Эта находка утверждает нас в том, что для христиан такая система закономерностей мер была символичной и использовалась в сакральном искусстве.

18 Василий Великий, архиепископ Кессарии Кападокийской. Творения. – М., 1993; Ч. IV. – 406 с. C. 266.

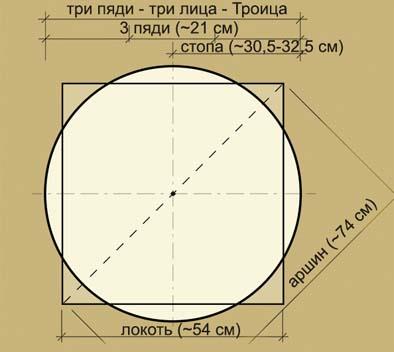
Рис. 2. Символическо-богословская основа тройной системы мер, решающей задачу «квадратура круга», применявшуюся в древнерусском храмостроении X–XV вв.

По немного другим мерам, эта же цепочка в физических размерах может выглядеть немного укрупнённо: локоть 0,54-0,56 м (от Пояса Христа 1,08–1,1 м по вычислению Б.А. Рыбакова, усреднённых длины и ширины целыми мерами внутри церкви Успения Пресвятой Богородицы Киево-Печёрского монастыря (1073 г.); аршин 0.74 м; стопа византийская 0,33 м по Р.Оустерхауту [16, с. 29]; пядь 0,22 м. Оустерхаут пишет, что «в рукописи по геометрии XI или XII века, повторяющей более ранних авторов, затрагивается ряд архитектурных проблем», которые иллюстрируются разнообразными схемами, и «они переполнены ошибками, а все числа округлены до предела», а сопровождающие схемы не масштабны…» [16, с.86-87]. Поэтому принимаемые нами округления в символических схемах можно считать вполне допустимым, ввиду важности для христианского зодчего смыслов и образов, а не мелочей и десятых частей от сантиметров.

Эту антропоморфную систему соответствий мер длины можно продолжить. Так, при удвоении изначальных мер, получаем: сторона квадрата, равная локтю (0,52-0,54 м), взятая два раза, даёт нам меру Пояс Христа (1,05-1,08 м); диагональ, равная аршину (0,71-0,74 м), – двухаршинную сажень или Тмутараканскую (1,42-1,48 м); пядь (0,21– 0,215 м), взятая 6 раз – это меньшая сажень по Пилецкому А.А. (1,26-1,31 м). При утроении исходных размеров: сторона квадрата становится равной 1,56-1,62 м; диагональ – Византийская сажень (2, 12-2, 22 м); диаметр круга – 9 пядей (0,21-0,215 м), т.е. – 1,89– 1,93 м («сажень без чети», и, действительно, для неё не надо парной меры, так как она диаметр круга). То есть, зная, сколько локтей (0,52 м) в стороне квадрата, можно утроением этого числа «во Славу Святой Троицы» взять пядей «распахнутых» как «небо» (0,21 м) и получить диаметр круга «неба», равного квадрату по площади. Для вычисления радиуса этого круга достаточно взять стопу столько же раз, сколько локтей в квадрате.

Такое сложение малых частей проводилось ранее исследователями: Афанасьевым К.Н. (1954, 2002), Рыбаковым Б.А. (1949, 1957, 1974), Шевелёвым И.Ш. (1963, 2009), Пилецким А.А. (1980), Бондаренко И.А. (1988) и другими. Ими были описаны закономерности деления саженей на малые составляющие, такие как аршины, локти, стопы, пяди и т.д. Например, аршины, взятые много раз в каком-то количестве, начинают быть равными локтям, взятым несколько раз. То есть 3-х аршинная мера – это сажень 2,12 м, которая, в свою очередь, является 4-х локтевой (0,53 м), а 4-х аршинная является городовой саженью (2,84 м), десятистопная сажень (3,15-3,25 м) является одновременно состоящей из 6 локтей (0,52-0,54 м) и из трёх Поясов Христа (1,05-1,08 м). Расстояние в двенадцать аршин (0,71-0,74 м) могут делиться на четыре сажени по 2,10-2,17 м, или на три сажени городовых по 2,84 м. Все сажени кратны более мелким, таким как стопы, пяди и вершки. Поэтому такая троичная систематизация через решение геометрической задачи «квадратура круга» представляет пример упорядочивания и адаптации ранее существовавших единиц измерения для упрощения использования в размерении пропорций в храмах в тесной связи с богословием.

Пояс Христа и геометрическая запись богословского понятия св. Троицы

Вначале коснемся вопроса восстановления названия полусажени (1,05-1,08 м) как «Пояса Сына», точно цитируя летопись, или «Пояс Иисуса Христа», поскольку оставлять название из времён «материалистического» СССР («Пояс Шимона») представляется нецелесообразным, в целях сохранения смыслов древнерусских зодчих, которые могли бы передаваться и современным архитекторам, через реконструкцию названий древнерусских мер.

Византинист Роберт Оустерхаут описывает сажень 2,12 м, использовавшуюся в Византии при размерении храмов, называя её оргией [16, с.74], которая делилась на 9 спитам, каждая из частей при этом отмечалась бечёвкой, а впоследствии – кольцами. Оргии по десять штук объединялись под названием схонион, что в сумме составляло 20 Поясов Иисуса Христа (1,05 м), которыми размерялась внутренняя ширина собора Успения Пресвятой Богородицы Киево-Печерской лавры (1073 г.), о чём повествует летопись (Киево-Печёрский Патерик, 1073). После середины XI века длина используемой оргии увеличилась до 2,17 м. Эта сажень (2,12-2,17 м) использовалась в России до начала XX века [17] и донесла до нас глубокое богословское понятие через своё деление на три части (аршина), и, в тоже время, состоящая из двух Поясов Иисуса Христа (1,05-1,08 м).

Это проявление философского понимания мироустройства, где первопричина есть Бог и св. Троица (рис. 3).

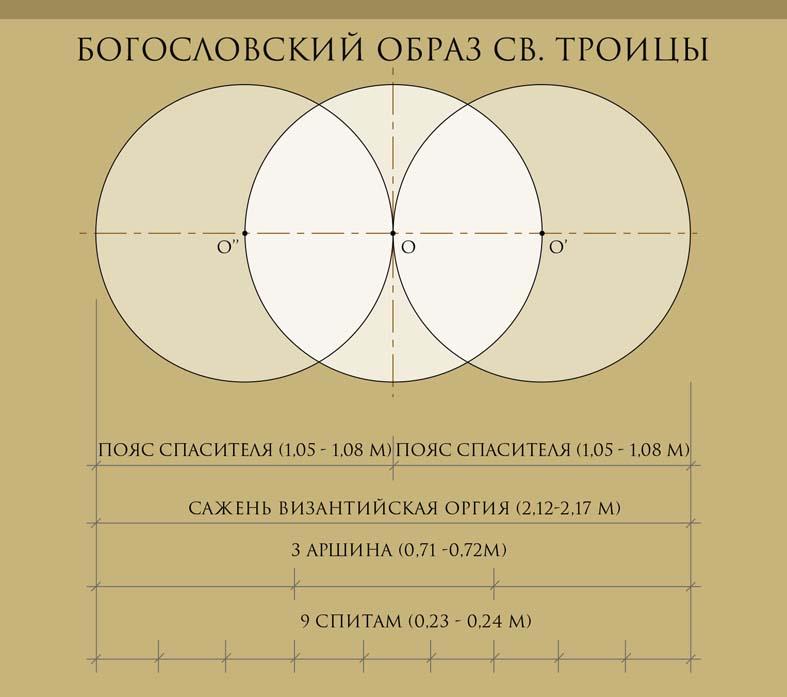
Рис. 3. Геометрический анализ меры Пояс Иисуса Христа, раскрывающий богословские понятия св. Троицы и двойной природы Иисуса Христа, применявшийся в древнерусском храмостроении X–XV вв. Условные обозначения: O – центр серединного круга; O’, O’’ – центры двух дополнительных кругов, равных центральному, строящиеся для последующего размерения квадрата, равного кругу по площади («квадратура круга»).

При таком философском понимании трёхаршинной сажени (2,12-2,17 м), становится понятным её «устойчивое» использование в размерении внутренней ширины древнерусских храмов как образа св. Троицы. Также встречается использование полусажени от неё, именуемой в российской метрологии как Пояс Шимона, а по нашему предложению – «Пояс Христа» (1,05-1,08 м). В таком двухчастном делении проявляется философский догмат о двойной природе Иисуса Христа. То есть символически одна половина сажени, посвящённой св. Троице, относится к одному из свидетельств земной жизни Бога, как его пояса, а другая, соответственно, к его божественной сущности. Если посмотреть на геометрическое начертание богословского понятия св. Троицы, использовавшегося при размерении внутренней ширины трёх центральных нефов [2], то можно понять, почему символизирующая Троицу сажень делится на две части, для выявления двух равнозначных природ Христа, а не на три. Так как суммарная фигура, изображающая св. Троицу, имеет именно два диаметра круга, третий объединяет эти два круга. Таким образом, богословие, записанное как геометрией, так и арифметикой, выявляет множество смыслов, которые сначала не видны, подобно тому, как писал Феофил Антиохийский (II в.) в Послании к Автолику: «…вид Бога неописуем и неизъясним, ибо не может быть видим плотскими глазами» [18].

Представляется интересным в этой связи проанализировать построение интерьера храма на горе Нево (IV в.) [19, 20]. В материальных формах интерьера – абрисе апсидных выкружек триконха – можно увидеть три круга, четвёртый же, равный им проявляющийся при геометрическом анализе, находится в центре (рис. 4). То есть, три сплетённых круга – это богословский символ св. Троицы, как ранее было выяснено по трактату святителя Григория Богослова (IV в.). А четвёртый круг с востока, выстраивающий внутренний абрис апсиды как символической пещеры земного воплощения Бога, равен по диаметру каждой из трёх, то есть равнозначен им и это образ человеческой природы Иисуса Христа, рассказ о том, что он как Бог, так и Человек.

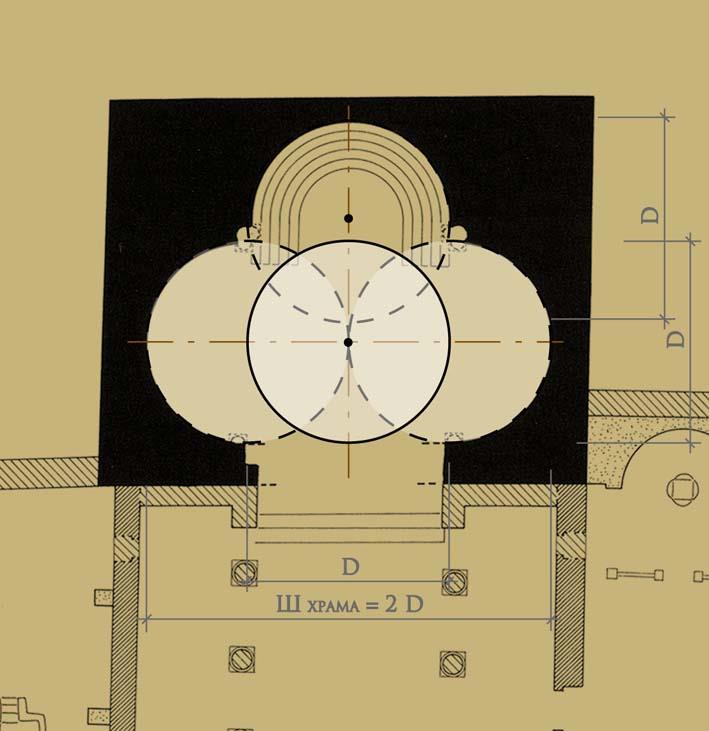
Рис. 4. Геометрический анализ плана триконха на горе Нево в Палестине (IV в.). Условные обозначения: D – диаметр круга, выстраивающего апсидные выкружки; Ш – ширина триконхиального храма в интерьере, равная двум диаметрам круга

Таким образом, мера «Пояс Иисуса Христа» (1,05-1,08 м) как половина от византийской оргии (2,12-2,17 м), доносит нам из глубины веков глубокий философский смысл, использовавшийся в храмостроении, повествуя о геометрическом образе богословского понятия св. Троицы, двойной природы Христа и девятичастном символическом делении (3×3).

Символические дроби в пропорциях «мира видимого» и «невидимого» в храме

Ранее, при анализе геометрического построения христианских древнерусских храмов нами были выявлены символические дробные деления, использовавшиеся для размерения символических зон в интерьере храмов, таких как «мир видимый» от западной стены структурного ядра до иконостаса и «мир невидимый» от иконостаса до восточной стены в центральной апсиде [3]. Для этого брался шнур, равный внутренней ширине трёх центральных нефов, делился на четыре части, из которых потом брались три, и откладывалось расстояние от западной стены до иконостаса. Таким образом получалось размерить символическое пространство в структурном ядре храма, называемое «мир видимый». Последний из отрезков опять делился на четыре части, тремя из которых размерялась глубина алтаря – расстояние от иконостаса до восточной стены в интерьере. То есть, получалась символическая зона, именуемая «мир невидимый» (рис. 5). Такое соотношение используемых четырёх частей для «мира земного», а для размерения «мира невидимого» трёх из них, является философским закреплением догмата о двойной природе Иисуса Христа: он и Бог, и рождался человеком (3 + 1 = 4), где 3 – Троица, а 1 земное воплощение Бога. Здесь можно ещё раз упомянуть храм на горе Нево, где при построении внутреннего пространства триконха использованы четыре равных круга, три из которых сплетены в образ св. Троицы, а четвёртый находится восточнее и им обрисовывается апсида святой пещеры (рис. 4).

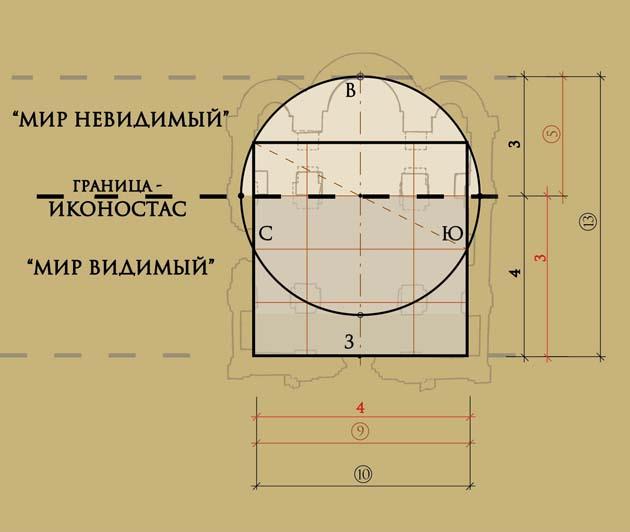
Рис. 5. Использование символических дробей в размерении «мира видимого» и «невидимого» в структурном ядре древнерусских храмов X-XV вв. с пропорциями 10:13, на примере плана церкви св. Бориса и Глеба в Кидекше (1152 г.)

Далее обратимся к вопросу о двух вариантах возможного символического перечисления в христианских сооружениях. Один – это символическое изображение богословского понятия через геометрический символ, как об этом писал святитель Григорий Богослов архиепископ Константинопольский (IV в.), отмечая, что математика не может объяснить, например, такое понятие как св. Троица, так как то, что можно сложить, то можно и разъединить. Святая Троица же Едина и, в тоже время, имеет три лица. Поэтому в христианском храмостроении для символической записи того, что посередине храма во внутренних габаритах трёх нефов пребывает св. Троица, использовалась геометрическая запись из трёх плотно сплетённых кругов, центры которых находились на расстоянии одного радиуса друг от друга на оси Север-Юг, проходящей через центр подкупольного квадрата. В то же время хорошо известны использования посвящения во Имя св. Троицы и использование троичного перечисления, например, три апсиды или три окна в центральной апсиде, изображающие собой свет св. Троицы. То есть три элемента не есть богословский рассказ о сущности св. Троицы, а лишь посвящение ей. Таким образом, существуют два варианта упоминания: первый – это объяснение сущности философского понятия, а второй – посвящения.

Поэтому, возвращаясь к размерению структурного ядра древнерусского храма с пропорциональным отношением ширины к длине как 10:13 можно констатировать, что при этом использовалось практическое деление целого шнура на четыре части, из которых потом брались три во имя св. Троицы, к которым прибавлена одна часть земного воплощения Спасителя. Такое же построение пропорций было описано ранее, например, в плане храма на горе Нево, где внешний абрис стен, представляющий из себя прямоугольник, имеет отношение ширины по оси Север-Юг к длине по оси Восток Запад как 4:3. Если учитывать тот факт, что внешний контур здания символически соотносился с образом земной жизни, то есть «миром видимым», то усматривается логическая связь с размерением именно «мира видимого» как зоны в структурном ядре храма от входа до иконостаса.

Возникает также предположение о возможном существовании взаимосвязанных построений, например, богословской пропорции 8:9 через символическую дробность 3/4, где 4 части – символ «земной жизни», взятые два раза (4+4), относятся к трём частям, «во Имя св. Троицы», взятым три раза (3+3+3). Это символизирует отношение «земного» квадрата к «небесному» кругу, как диаметра круга, равного этому квадрату по площади. К этой паре в строительстве необходима и диагональ квадрата, чтобы получился не ромб. Длина диагонали – 11. То есть, продолжая выявленную закономерность при дробном размерении структурного ядра древнерусского храма, где вся длина представляет собой цепочку последовательных отложений частей целого как 4+3=7, символизирующую святую Седмицу [3], чтобы получить 11, надо к 7 прибавить 4. То есть для практического построения на местности может быть достаточно дробей ¾, где сторона квадрата есть 4+4=8, диаметр круга 3+3+3=9, а диагональ – 4+3+4=11 (рис. 6).

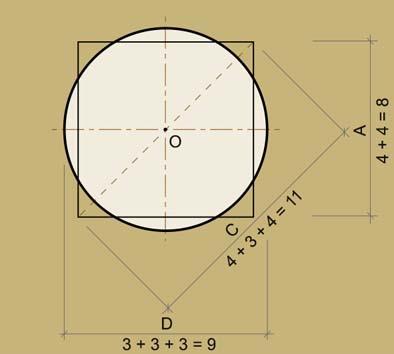
Рис. 6. Символическое решение дробями задачи «квадратура круга», использовавшейся в размерениях древнерусских храмов X-XV вв. Условные обозначения: A – сторона квадрата, равного по площади кругу; D – диаметр круга, равного квадрату по площади; С – диагональ квадрата, равного кругу по площади; O – центр круга и квадрата

Глубину алтаря можно размерить пропорцией 5/9, где 5 – глубина алтаря, а 9 – внутренняя ширина трёх центральных нефов в храме. Если вспомнить, что сажень оргия (2,12–2,17 м) делилась, в свою очередь, на 9 частей, то использование именно такой дроби становится вполне объяснимым (рис. 5). При этом по ширине структурного ядра храма символически записывается через геометрию богословский образ св. Троицы. Поэтому три, взятое три раза (3×3=9) для такой пропорции для последующего размерения глубины алтаря, как образа Священной пещеры – свидетельства земного воплощения Бога как пяти частей, что является очень понятным для христианина. Так как пять – это земной символ суммы Иисуса Христа и четырёх Евангелистов.

В различных способах практического размерения на местности храмовых построек наблюдается многогранное понимание геометрических и числовых символов в тесной связи с богословием.

Выводы

Таким образом, реконструированные в выполненном исследовании геометрические схемы: «квадратуры круга», выравнивающей между собой по площади круг и квадрат; «св. Троицы», как плотно сплетённых трёх кругов; дробей, наполненных символическим смыслом, использовавшихся в древнерусском храмостроении X–XV веков, позволяют раскрывать глубинные многогранные смыслы и систематизации древних саженей и других мер длины в их тесной связи с философией и мировоззрением Христианства. Найденная взаимосвязь геометрических построений в храмостроении с историческими и летописными упоминаниями о священных и антропоморфных мерах длины открывает возможность к дальнейшему поиску геометрических закономерностей, кроющихся в древнерусских саженях и определяющих архитектурные формы и детали памятников древнерусской архитектуры.

Источники иллюстраций

Рис. 1-3, 6. Схемы автора.

Рис. 4. Фрагмент плана по И.Ш. Шевелёву (2009) с графическим анализом автора. Рис. 5. План по К.Н. Афанасьеву (2002) с графическим анализом автора.

Литература

1. Венгерова М.Э. Решение задачи «квадратуры круга» в геометрическом пропорционировании древнерусских храмов X-XV веков // Architecture and Modern Infrmation Technologies. – 2017. – №1(38). – С. 137-148 :http://marhi.ru/AMIT/2017/1kvart17/vengerova/index.php

2. Венгерова М.Э. «Животворящий столп» как основа пропорционирования древнерусских храмов X – XV веков // Architecture and Modern Information Technologies. – 2018. – №1(42). – С. 24-46 : http://marhi.ru/AMIT/2018/1kvart18/01_vengerova/index.php

3. Венгерова М.Э. К выяснению сущности пропорций структурных ядер в древнерусских храмах X – XV веков // Architecture and Modern Infrmation Technologies. – 2018. – №3(44). – С. 331-345 : http://marhi.ru/AMIT/2018/3kvart18/20_vengerova/index.php

4. Ерм. Пастырь // Легеев М.В., свящ. Патрология. Период Древней Церкви: с хрестоматией: [учебн. пособие] / свящ. Михаил Легеев. – СПб.: Изд-во СПбПДА, 2015. – 592 с.

5. Соловьёв Петр, протоиерей. Описание Новгородскаго Софийскаго собора. – СПб, 1852. – 244 с.

6. Robert Odell Bork. The geometry of creation : architectural drawing and the dynamics of gothic design. – Farnham: Asngate, 2011. – 462 s.

7. ГНИИМА им. А.В. Щусева, РV № 4767. Церковь Рождества в Перынском скиту Юрьева монастыря близ г. Новгорода, XIII(?) век. Специальные проектно– реставрационные мастерские комитета архитектуры при СМ СССР для Управления по делам архитектуры СМ РСФСР, 1949.

8. ГНИИМА им. А.В. Щусева, РV № 3869. Собор Успения Пресвятой Богородицы во Владимире (1158-1161 гг. Перестр. 1185-1189 гг.). План контрольный чертёж. По обмерам арх-ров Брайцевой О.И., Шевченко Н.Б., Ульяшова В.С., 1947.

9. ГНИИМА им. А.В. Щусева, Р V 2503/1. Церковь Спаса на Нередице. План на отм. 0.00. Проект реставрации, Специальная Проектно-реставрационная мастерская комитета по делам архитектуры при СМ СССР, нач. мастерской арх. Давыдов С.Н., 1947-48.

10. ГНИИМА им. А.В. Щусева, РV 3855/1. Собор св. Софии в Новгороде. Обмерный план, рук. Кацнельсон Р.А., 1946-47 гг.

11. ГНИИМА им. А.В. Щусева, РV №5188/1. Николо-Дворищенский собор в Новгороде (1113 г.). План по полу храма. 1947-48.

12. Зубов В.П. Труды по истории и теории архитектуры. – М.: Искусствознание, 2000. – 528 с.

13. Венгерова М.Э. Геометрические построения пропорций, связанные с шириной храмов Древней Руси X – XV веков // Наука, образование и экспериментальное проектирование, Тезисы докладов, международной научно-практической конференции профессорско-преподавательского состава и молодых учёных и студентов, 4-8 апреля 2016 г. – М.: МАРХИ, 2016. – Т.1. – С. 32-33.

14. Святитель Симеон, архиепископ Солунский. Объяснение священных обрядов и Таинств Церкви. – М.: Благовест, 2013. – 640 с.

15. Иоанн Мосх, блаженный. Луг духовный: достопамятные сказания о подвижничестве святых и блаженных отцов / Блаженный Иоанн Мосх. Перев. С греч. Прот. М.И. Хитрова. – М.: Сибирская Благозвонница, 2016. – 527 с.

16. Оустерхаут Роберт. Византийские строители. Пер.: Беляев Л. А.; ред. и коммент. Беляев Л. А., Ивакин Г. Ю. – Киев – Москва: КОВРИН ПРЕСС, 2005. – 332 c.

17. ГНИИМА им. А.В. Щусева, РV № 1834. Церковь Бориса и Глеба на Смядыне близ г. Смоленска. План откопанного храма на Смядыне. Чертила Е.Н. Клетнова, 1907.

18. Успенский Л.А. Богословие иконы православной Церкви. Изд-во Западно– европейского экзарха, Московский патриархат. Репринтное издание. – М.: Ликом, 1996. – 464 с.

19. Severin H.-G., Grossmann P. Frühchristlihe und Byzantinische bauten in südostlichen Lykien. Tübingen: Ernst Wasmuth Verlag, 2003. – 180 s.

20. Венгерова М.Э. Философско-богословские споры и понятия в геометрическом построении пропорций христианских храмов IV – XV веков // Социально-Гуманитарное обозрение. – М.: Общество с ограниченной ответственностью «Издательство «Юнити-Дана», 2018. – № 3. – Том 3. – С. 55-62 : https://elibrary.ru/item.asp?id=35385245